Підмножина

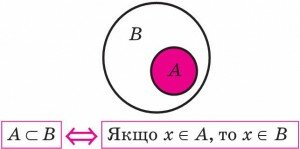
Якщо кожен елемент однієї множини A є елементом множини B, то кажуть, що перша множина A є підмножиною  множини B.Це записують так: A ⊂ B.

Наприклад, {1; 2} ⊂ {0; 1; 2; 3}, N ⊂ Z  (оскільки будь-яке натуральне число — ціле), Z ⊂ Q  (оскільки будь-яке ціле число — раціональне),  Q  ⊂  R  (оскільки будь-яке раціональне число — дійсне).

Вважають, що завжди ∅ ⊂ A, тобто порожня множина є підмножи-ною будь-якої непорожньої множини.

Інколи замість запису A ⊂ B використовують також запис A ⊆ B, якщо множина A або є підмножиною множини B, або дорівнює множині B. Наприклад, A ⊆ A.

Співставимо означення рівності множин з означенням підмножини.

Якщо множини А і В рівні, то:

1. кожний елемент множини А є елементом множини B, отже, А — підмножина В
   (A ⊆ B);
2. кожний елемент множини В є елементом множини А, отже, В — підмножина А
   (B ⊆ A).

Таким чином, дві множини рівні, якщо кожна з них є підмножиною іншої.

Інколи співвідношення між множинами зручно ілюструвати за допомогою кругів (які часто називають кругами Ейлера-Венна).