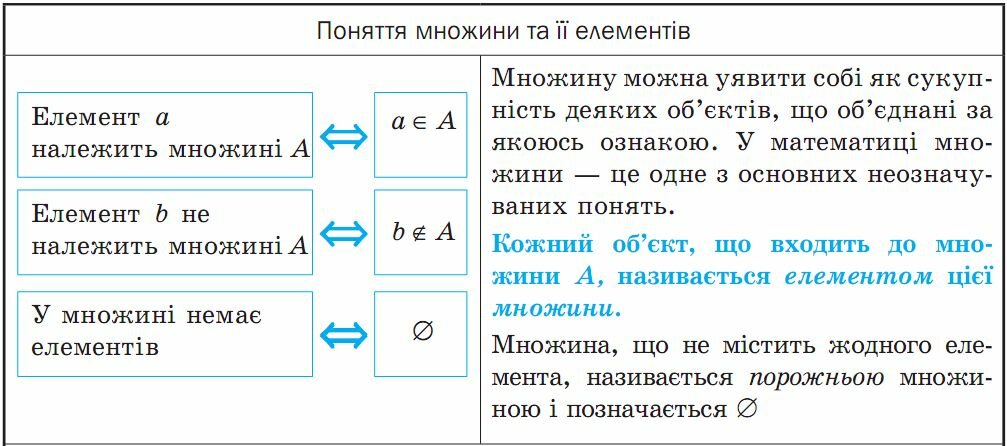
Множини. Елементи множин
Одним з основних понять, які використовують у математиці, є поняття множини. Для нього не дають означення. Можна пояснити, що множиною називають довільну сукупність об’єктів, а самі об’єкти — елементами даної множини. Так, можна говорити про множину учнів у класі (елементи — учні), множину днів тижня (елементи — дні тижня), множину натуральних дільників числа 6 (елементи — числа 1, 2, 3, 6) тощо.
У курсах алгебри та алгебри і початків аналізу найчастіше розглядають множини, елементами яких є числа, і тому їх називають числовими множинами .
Як правило, множини позначають великими літерами латинського алфавіту. Наприклад, якщо множина М складається із чисел 1; 2; 3, то її позначають так: М = {1; 2; 3}. Той факт, що число 2 входить до цієї множини (є елементом даної множини М), записують за допомогою спеціального значка ∈ так: 2 ∈ М; а те, що число 5 не входить до цієї множини (не є елементом даної множини), записують так: 5 ∉ М.
Можна розглядати також множину, яка не містить жодного елемента, — порожню множину.
Наприклад, множина простих дільників числа 1 — порожня множина.
Позначення множин
Для деяких множин існують спеціальні позначення:
- порожню множину позначають символом ∅;
- множину всіх натуральних чисел — літерою N;
- множину всіх цілих чисел — літерою Z;
- множину всіх раціональних чисел — літерою Q;
- множину всіх дійсних чисел — літерою R.
Множини бувають скінченні і нескінченні залежно від того, яку кількість елементів вони містять. Так, множини А = {7}; M = {1; 2; 3} — скінченні, бо містять скінченне число елементів, а множини N, Z, Q, R — нескінченні.
Множини задають або за допомогою переліку їх елементів (це можна зробити лише для скінченних множин), або за допомогою опису, коли задається правило — характеристична властивість, яке дозволяє визначити, належить чи ні даний об’єкт розглядуваній множині. Наприклад, множина А = {–1; 0; 1} задана переліком елементів, а множина B парних цілих чисел — характеристичною властивістю елементів множини. Останню множину інколи записують так: B = {b | b — парне ціле число} або так: B = {b | b = 2m, де m ∈ Z} — тут після вертикальної риски записана характеристична властивість. (запис m ∈ Z означає, що m приймає будь-яке ціле значення, що також можна записувати так: m = 0; ±1; ±2; …)
У загальному вигляді запис множини за допомогою характеристичної властивості можна подати так: A = {x | P (x)}, де P (x) — характеристична властивість.
Наприклад, {x | x2 – 1 = 0} = {–1, 1}, {x| x ∈ R і x2 + 1 = 0} = ∅.

 (14 глосів, оцінка: 4,29)
(14 глосів, оцінка: 4,29)