Піраміда

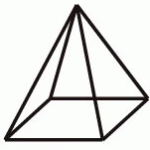
Пірамідою називається многогранник, одна грань якого — довільний многокутник, а інші грані — трикутники, що мають спільну вершину.

Для задання піраміди достатньо будь-який многогранний кут перетнути довільною площиною.

Для зображення піраміди вибираємо многокутник (довільний) і точку поза площиною цього многокутника. Сполучаємо задану точку з усіма вершинами многокутника.

Грань піраміди, що задає многокутник, називають основою піраміди.

Інші грані називають бічними гранями піраміди, і вони є трикутниками.

Спільна вершина трикутників називається вершиною піраміди.

Позначають піраміду, починаючи з вершини SABCD …, і називають n-кутною пірамідою залежно від кількості вершин многокутника.

Ребра, що сполучають вершину піраміди з вершинами основи, називають бічними ребрами.

Точка S — вершина піраміди;

многокутник ABCDEFK … — основа піраміди;

Δ SAB, Δ SBC, Δ SCD, ΔSDE, … — бічні грані піраміди;

відрізки SD, SB, SC, SD, … — бічні ребра піраміди.

Перпендикуляр, проведений із вершини піраміди на площину основи, називається висотою піраміди, SO ⊥(ABC)  —висота піраміди, позначається SO  =  H.

Діагональна площина — площина, яку проведено через будь-яку з діагоналей основи і вершину піраміди, а переріз піраміди цією площиною називають діагональним перерізом — це трикутник.

Класифікація пірамід

Правильна піраміда

Неправильна піраміда

Зрізана піраміда

Піраміда називається неправильню, якщо в її основі лежить неправильний багатокутник або, якщо в її основі лежить правильний багатокутник, але
вершина піраміди не проектується у центр основи піраміди.

Залежність кількості ребер, вершин і граней піраміди від кількості кутів

Кутів	Вершин	Граней	Ребер
n = 3	4	4	6
n = 4	5	5	8
n-кутна	n + 1	n + 1	2n