Сполуки без повторень. Комбiнацiї

Комбiнацiї без повторень — це сполуки, якi мають такi характернi ознаки:

1. Елементи у сполуцi не повторюються.
2. Кiлькiсть мiсць (m) у сполуцi не бiльша нiж кiлькiсть елементiв (n), якi претендують на цi мiсця (m ≤ n).
3. Порядок розташування елементiв у сполуцi не має значення.

Кiлькiсть комбiнацiй обчислюють за формулою  

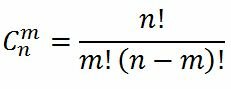
C_n^m = n! / (m!·(n — m)!)

Задача 1

Іван, Андрiй, Олег, Сергiй i Вiктор жеребкуванням призначають двох чергових у класi. Скiльки iснує варiантiв такого вибору?

Розв’язання

Оскiльки обов’язки в обох чергових однаковi, а кiлькiсть хлопцiв менша за кiлькiсть чергових, то iснує

C₅² = 5! / (2!·(5 — 2)!) = 10 варiантiв призначення чергових.

Вiдповiдь. 10 варiантiв.

Задача 2

У змаганнях з баскетболу беруть участь 10 команд, з яких тiльки чотири перших змагатимуться у фiнальнiй частинi. Скiльки iснує варiантiв складу фiнальної четвiрки?

Розв’язання

Не має значення, яке з чотирьох перших мiсць посяде команда. Усього 10 команд, кiлькiсть мiсць для фiналiстiв дорiвнює 4, отже, iснує

C₁₀⁴ = 10! / (4!·(10 — 4)!)= 210 варiантiв складу фiнальної четвiрки.

Вiдповiдь. 210 варiантiв.